gerak harmonik

Gerak harmonik sederhana adalah gerak bolak - balik benda melalui suatu titik keseimbangan tertentu dengan banyaknya getaran benda dalam setiap sekon selalu konstan^[1].

 Jenis, Contoh, dan Besaran Fisika pada Gerak Harmonik Sederhana

Jenis Gerak Harmonik Sederhana

Gerak Harmonik Sederhana dapat dibedakan menjadi 2 bagian, yaitu^[1] :

• Gerak Harmonik Sederhana (GHS) Linier, misalnya penghisap dalam silinder gas, gerak osilasi air raksa / air dalam pipa U, gerak horizontal / vertikal dari pegas, dan sebagainya.
• Gerak Harmonik Sederhana (GHS) Angular, misalnya gerak bandul/ bandul fisis, osilasi ayunan torsi, dan sebagainya.

Beberapa Contoh Gerak Harmonik Sederhana

• Gerak harmonik pada bandul

Ketika beban digantungkan pada ayunan dan tidak diberikan gaya, maka benda akan dian di titik keseimbangan B^[2]. Jika beban ditarik ke titik A dan dilepaskan, maka beban akan bergerak ke B, C, lalu kembali lagi ke A^[2]. Gerakan beban akan terjadi berulang secara periodik, dengan kata lain beban pada ayunan di atas melakukan gerak harmonik sederhana^[2].

• Gerak harmonik pada pegas

Semua pegas memiliki panjang alami sebagaimana tampak pada gambar^[2]. Ketika sebuah benda dihubungkan ke ujung sebuah pegas, maka pegas akan meregang (bertambah panjang) sejauh y. Pegas akan mencapai titik kesetimbangan jika tidak diberikan gaya luar (ditarik atau digoyang)^[2].

 Besaran Fisika pada Ayunan Bandul

Periode (T)

Benda yang bergerak harmonis sederhana pada ayunan sederhana memiliki periode^[3]. Periode ayunan (T) adalah waktu yang diperlukan benda untuk melakukan satu getaran. Benda dikatakan melakukan satu getaran jika benda bergerak dari titik di mana benda tersebut mulai bergerak dan kembali lagi ke titik tersebut. Satuan periode adalah sekon atau detik^[3].

Frekuensi (f)

Frekuensi adalah banyaknya getaran yang dilakukan oleh benda selama satu detik, yang dimaksudkan dengan getaran di sini adalah getaran lengkap^[3]. Satuan frekuensi adalah hertz^[3].

Hubungan antara Periode dan Frekuensi

Frekuensi adalah banyaknya getaran yang terjadi selama satu detik. Dengan demikian selang waktu yang dibutuhkan untuk melakukan satu getaran adalah^[3] :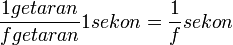



Selang waktu yang dibutuhkan untuk melakukan satu getaran adalah periode. Dengan demikian, secara matematis hubungan antara periode dan frekuensi adalah sebagai berikut^[3] :

Amplitudo

Pada ayunan sederhana, selain periode dan frekuensi, terdapat juga amplitudo. Amplitudo adalah perpindahan maksimum dari titik kesetimbangan^[3].

Gaya Pemulih

Gaya pemulih dimiliki oleh setiap benda elastis yang terkena gaya sehingga benda elastis tersebut berubah bentuk^[4]. Gaya yang timbul pada benda elastis untuk menarik kembali benda yang melekat padanya di sebut gaya pemulih^[4].

Gaya Pemulih pada Pegas

Pegas adalah salah satu contoh benda elastis^[4]. Oleh sifat elastisnya ini, suatu pegas yang diberi gaya tekan atau gaya regang akan kembali pada keadaan setimbangnya mula- mula apabila gaya yang bekerja padanya dihilangkan^[4]. Gaya pemulih pada pegas banyak dimanfaatkan dalam bidang teknik dan kehidupan sehari- hari^[4]. Misalnya di dalam shockbreaker dan springbed^[4]. Sebuah pegas berfungsi meredam getaran saat roda kendaraan melewati jalan yang tidak rata^[4]. Pegas - pegas yang tersusun di dalam springbed akan memberikan kenyamanan saat orang tidur^[4].

Hukum Hooke

Jika gaya yang bekerja pada sebuah pegas dihilangkan, pegas tersebut akan kembali pada keadaan semula^[5]. Robert Hooke, ilmuwan berkebangsaan Inggris menyimpulkan bahwa sifat elastis pegas tersebut ada batasnya dan besar gaya pegas sebanding dengan pertambahan panjang pegas^[5]. Dari penelitian yang dilakukan, didapatkan bahwa besar gaya pegas pemulih sebanding dengan pertambahan panjang pegas. Secara matematis, dapat dituliskan sebagai^[5] :

, dengan k = tetapan pegas (N / m)

Tanda (-) diberikan karena arah gaya pemulih pada pegas berlawanan dengan arah gerak pegas tersebut.

[sunting] Susunan Pegas

Konstanta pegas dapat berubah nilainya, apabila pegas - pegas tersebut disusun menjadi rangkaian^[5]. Besar konstanta total rangkaian pegas bergantung pada jenis rangkaian pegas, yaitu rangkaian pegas seri atau paralel^[5].

• Seri / Deret

Gaya yang bekerja pada setiap pegas adalah sebesar F, sehingga pegas akan mengalami pertambahan panjang sebesar dan . Secara umum, konstanta total pegas yang disusun seri dinyatakan dengan persamaan^[5] :

, dengan k_n = konstanta pegas ke - n.

• Paralel

Jika rangkaian pegas ditarik dengan gaya sebesar F, setiap pegas akan mengalami gaya tarik sebesar dan , pertambahan panjang sebesar dan ^[5]. Secara umum, konstanta total pegas yang dirangkai paralel dinyatakan dengan persamaan^[5] :

k_total = k₁ + k₂ + k₃ +....+ k_n, dengan k_n = konstanta pegas ke - n.

Gaya Pemulih pada Ayunan Bandul Matematis

Ayunan matematis merupakan suatu partikel massa yang tergantung pada suatu titik tetap pada seutas tali, di mana massa tali dapat diabaikan dan tali tidak dapat bertambah panjang^[6]. Dari gambar tersebut, terdapat sebuah beban bermassa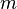 tergantung pada seutas kawat halus sepanjang dan massanya dapat diabaikan. Apabila bandul itu bergerak vertikal dengan membentuk sudut , gaya pemulih bandul tersebut adalah ^[6]. Secara matematis dapat dituliskan^[6] :

Oleh karena 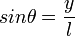, maka :